1.4. Corner Detection#

Motivation: shifting a window W in any direction should give a large change in intensity.

../../../_images/motivation.png

Math background#

Correlation#

Given \(\textbf{f - image, h - kernel}\)
cross correlation

\[ g=f \otimes h \]
\[g(i, j)=\sum_{k} \sum_{l} f(i+k, j+l) h(k, l)\]

auto correlation

\[g=f \otimes f \]
\[g(i, j)=\sum_{k} \sum_{l} f(i+k, j+l) f(k, l)\]

Normalized cross correlation

\[g_{N}(i,j) = \frac{\sum_{k} \sum_{l} f(i+k, j+l) h(k, l)} {\sqrt{\sum_{k} \sum_{l} f^{2}(i+k, j+l)} {\sqrt{\sum_{k} \sum_{l} h^{2}(k, l)}}}\]

Summed square difference (SSD)#

\[SSD(i,j)=\sum_{k} \sum_{l}(f(i+k, j+l)-h(k, l))^{2} \]
\[\begin{split} SSD(i,j)=\sum_{k} \sum_{l}\left({f(i+k, j+l)^{2}}-2 f(i+k, j+l) h(k, l) +{h(k, l)^{2}}\right) \\ = \sum_{k} \sum_{l}(-2 f(i+k, j+l) h(k, l))\end{split}\]

This is used in template matching. See Correspondence Matching

Relation between SSD and cross correlation#

\[\begin{split} \mathop{SSD(i,j)}\limits_{minimize} = \sum_{k} \sum_{l}{-2 h(i+k, j+l) f(k, l)} \\ \text{is equivalent to} \\ \mathop{\text{cross correlation(i,j)}} \limits_{maximize} = \sum_{k} \sum_{l} 2 h(i+k, j+l) f(k, l)\end{split}\]

Harris Corner Detection#

Error function#

Change in appearance of window \(w\) for the shift \((u, v)\):

\[E(u, v)=w(x,y)\sum_{(x, y) \in W}[I(x+u, y+v)-I(x, y)]^{2}\]

First-order Taylor approximation for small shifts \((u, v)\) :

\[I(x+u, y+v) \approx \color{red} {I(x, y)}+I_{x} u+I_{y} v\]

Let’s plug this into \(E(u, v)\):

\[\begin{split}E(u, v)\approx w(x,y)\sum_{(x, y) \in W}\left[I(x, y)+I_{x} u+I_{y} v-I(x, y)\right]^{2} \\ =w(x,y)\sum_{(x, y) \in W}\left[I_{x} u+I_{y} v\right]^{2}= w(x,y)\sum_{(x, y) \in W} I_{x}^{2} u^{2}+2 I_{x} I_{y} u v+I_{y}^{2} v^{2}\end{split}\]

Second moment matrix#

\[\begin{split}E(u, v) \approx w(x,y)(u^{2} \sum_{x, y} \color{red}{I_{x}^{2}}+ 2 u v \sum_{x, y} \color{red}{I_{x} I_{y}}+v^{2} \sum_{x, y} \color{red}{I_{y}^{2}}) \\ =\left(\begin{array}{ll}u & v\end{array}\right)M\left(\begin{array}{l}u \\ v\end{array}\right) \end{split}\]
\[\begin{split} M = \sum_{x, y}w(x,y)\left[\color{red}{\begin{array}{cc} I_{x}^{2} & I_{x} I_{y} \\ I_{x} I_{y} & I_{y}^{2}\end{array}}\right] = \left[\begin{array}{cc} A & B \\ B & C \end{array}\right]\end{split}\]

This matrix is weighted sum of nearby gradient information (could use Gaussian weighting).

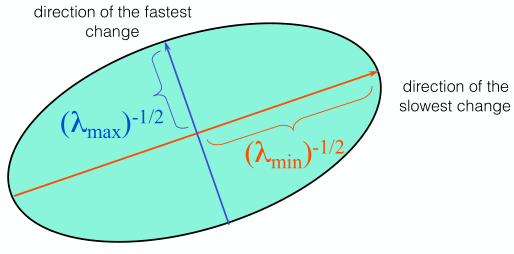
Visualization of a quadratic#

From previous section, \(E(u, v)\) is locally approximated by a quadratic form.

../../../_images/quadratic.png

Since \(M\) is symmetric, \(M\) could be diagonalized as

\[\begin{split} M=R^{-1}\left[\begin{array}{cc} \lambda_{1} & 0 \\ 0 & \lambda_{2} \end{array}\right] R\end{split}\]

Ellipse equation

Visualize \(M\) as an ellipse with axis lengths determined by the eigenvalues and orientation determined by \(R\)

\[\begin{split}\left(\begin{array}{ll}u & v\end{array}\right)M\left(\begin{array}{l}u \\ v\end{array}\right) = const\end{split}\]
../../../_images/ellipse.png

Eigenvalues interpretation#

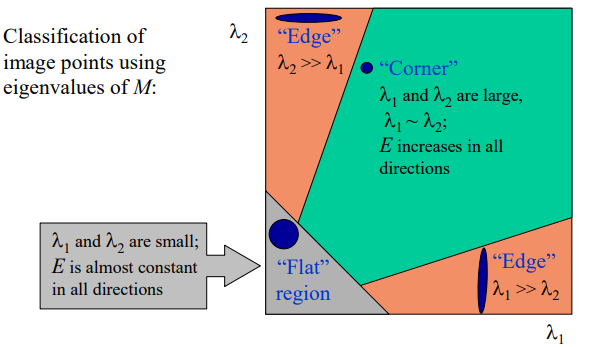
../../../_images/eigenvalue.png

Take-away

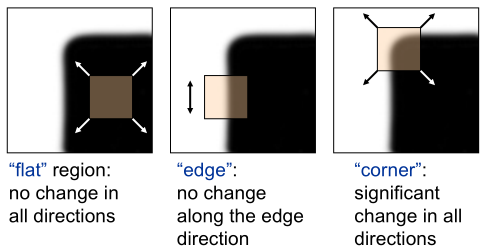
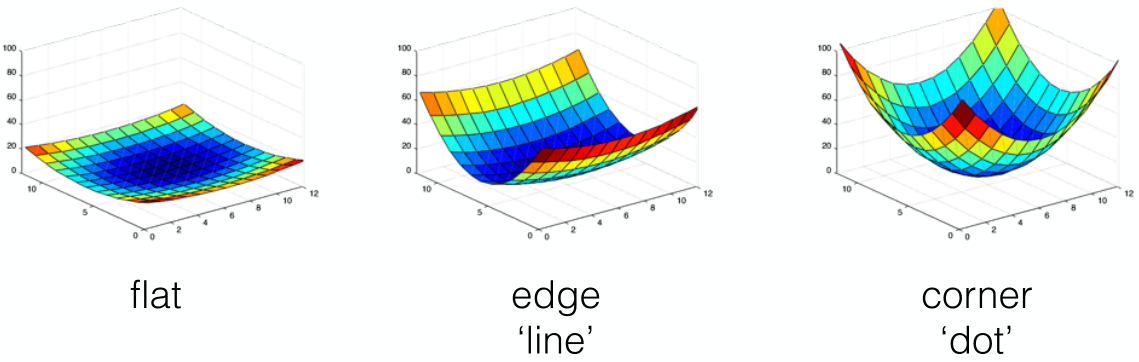
  • \(\lambda_{1}\) and \(\lambda_{2}\) both small: no gradient

  • \(\lambda_{1} \gg \lambda_{2}\) : gradient in one direction

  • \(\lambda_{1}\) and \(\lambda_{2}\) similarly large: multiple gradient directions, corner

Threshold on a function of eigenvalues#

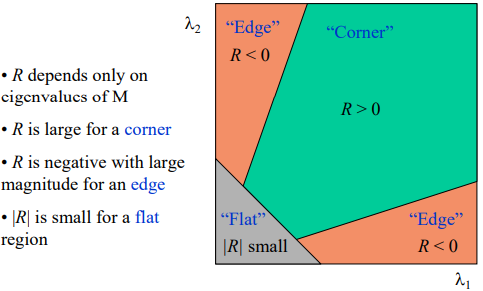
../../../_images/corner-response.png

Corner response \(R\)

\[\begin{split}\operatorname{det}(M)=\lambda_{1} \lambda_{2} = AB - C^2\\ \operatorname{trace}(\mathrm{M})=\lambda_{1}+\lambda_{2} = A + B\\ R = \operatorname{det}(M)- \alpha \operatorname{trace}(M)^{2} = \lambda_{1} \lambda_{2} - \alpha(\lambda_{1}+\lambda_{2})^{2}\end{split}\]

If these estimates are large, \(\lambda_{1}\) and \(\lambda_{2}\) are similarly large.

Summary#

Source code: C++ and Python implementation.

  • Intensity change in direction [u,v] can be expressed as a bilinear form:

\[\begin{split}E(u, v) \approx \left(\begin{array}{ll}u & v\end{array}\right)M\left(\begin{array}{l}u \\ v\end{array}\right)\end{split}\]

  • Compute corner response for each point in terms of eigenvalues of \(M\)

\[R = \lambda_{1} \lambda_{2} - \alpha(\lambda_{1}+\lambda_{2})^{2}\]

  • A good corner should have a large intensity change in all directions, i.e. R should be large positive.

Pipeline

  1. Compute partial derivatives \(I_{x}\) and \(I_{y}\) at each pixel

  2. Compute products of derivatives at every pixel

  3. Compute the sums of the products of derivatives at each pixel

  4. Compute second moment matrix \(M\) in a Gaussian window around each pixel

  5. Compute corner response function \(R=\operatorname{det}(M)-\alpha \operatorname{trace}(M)^{2}\)

  6. Threshold \(R\)

  7. Find local maxima of response function (NMS)

Implementaion in Jupyter#

Step1: Image gradients#

image = io.imread(fname="../../data/ass3/rice.png")
h,w = image.shape
# keep the output datatype to some higher forms
Ix = cv.Sobel(image,cv.CV_64F,1,0,ksize=1)
abs_Ix = np.absolute(Ix)
Ix_8u = np.uint8(abs_Ix)
Iy = cv.Sobel(image,cv.CV_64F,0,1,ksize=1)
abs_Iy = np.absolute(Iy)
Iy_8u = np.uint8(abs_Iy)

subplots([Ix_8u, Iy_8u], ['Ix', 'Iy'], 1,2)
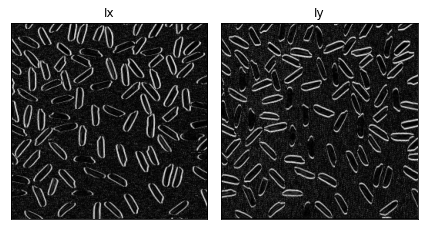
../../../_images/48f6c4fa770f1642c0af82ba2d369da1c91f65d51352b030ecee00ace70a5136.png

Step2: Second movement matrix M#

# Gaussian truncate window
kernel_size = 3
sigma = 0.5
Ixx = cv.GaussianBlur(Ix**2,(kernel_size,kernel_size), sigma)
Ixy = cv.GaussianBlur(Ix*Iy,(kernel_size,kernel_size), sigma)
Iyy = cv.GaussianBlur(Iy**2,(kernel_size,kernel_size), sigma)

Step3: Compute corner response function R#

offset = np.int8(kernel_size/2)
height, width = image.shape
corner_response = np.zeros((height, width))

# construct matrix elements
k = 0.02
for y in range(offset, height-offset):
    for x in range(offset, width-offset):
        A = np.sum(Ixx[y-offset:y+1+offset, x-offset:x+1+offset])
        C = np.sum(Iyy[y-offset:y+1+offset, x-offset:x+1+offset])
        B = np.sum(Ixy[y-offset:y+1+offset, x-offset:x+1+offset])
        det = (A * C) - (B**2)
        trace = A + C
        R = det - k*(trace**2)
        corner_response[y][x] = R

Step4: Corner response calculation and Non-maximum suppression#

# Response threshold 0.2*r_max 
R_max = np.max(corner_response)
Threshold_mask = corner_response > 0.2*R_max
# Non max suppression mask
NMS_mask = (corner_response == maximum_filter(corner_response, 5))
mask = Threshold_mask & NMS_mask
keypoints = np.argwhere(mask==True)

# compare with open source library
# keypoints = corner_peaks(corner_harris(image), min_distance=5, threshold_rel=0.02)

Intermediate results visualization#

Hide code cell source 
plt.figure(figsize=(15, 15))
imgs =  [Ix_8u, Iy_8u, Threshold_mask, mask, image]
titles = ['Ix', 'Iy', 'Thresholded corner response', 'Non-maximal suppression', 'Original image']

for i in range(5):
  plt.subplot(3,2,i+1),plt.imshow(imgs[i],'gray')
  plt.title(titles[i])
  plt.xticks([]),plt.yticks([])

plt.subplot(3,2,6)
plt.imshow(imgs[-1], cmap=plt.cm.gray)
plt.plot(keypoints[:, 1], keypoints[:, 0], color='red', marker='o',
        linestyle='None', markersize=2)
plt.title('Harris corners')
plt.xticks([]),plt.yticks([])
plt.tight_layout()
plt.show()
../../../_images/a1b1dd31011501ce065fc895b9153a34ce3ea67634397e89d005ea3b72a16c57.png

Invariance discussion#

Rotation invariance#

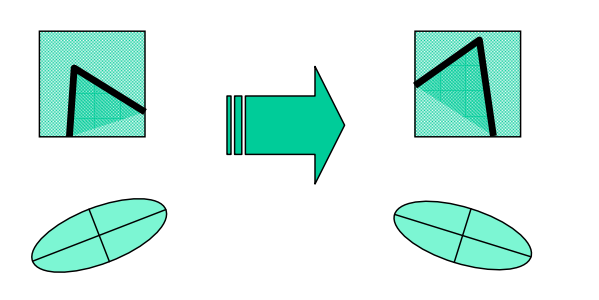
../../../_images/rotation.png

Corner response R is invariant to image rotation

Since Ellipse rotates but its shape (i.e. eigenvalues) remains the same.

Photometric transformations#

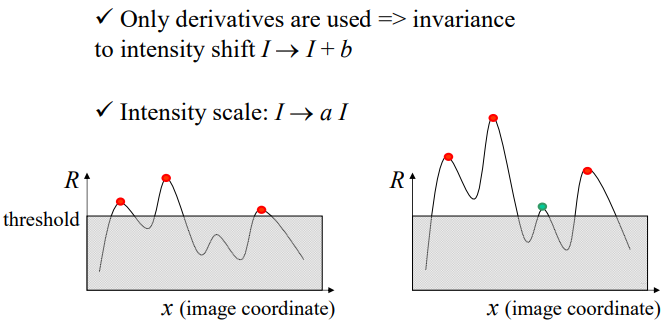
../../../_images/intensity.png

Partial invariance to additive and multiplicative intensity changes

Not invariant to changes in contrast.

Scale invariance#

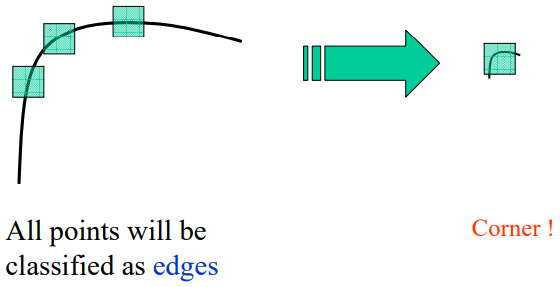
../../../_images/scale.png

Not invariant to scaling

Blob detection with Laplacian kernel could solve this.